# Глава 8. Вещественные числа Умение правильно работать с вещественными числами — черта, отличающая опытного разработчика от новичка. Почему число 123456789.00 в консоли выглядит как 123456792.00? Что будет, если в цикле прибавлять маленькие вещественные числа к очень большому? Какие есть способы для корректного сравнения дробных чисел? Если вы не знаете ответов на эти вопросы, то перед вами отличный шанс расширить кругозор. Если перечисленные вопросы кажутся вам легкими, то скучать все равно не придется: эта глава познакомит вас со спецификой вещественных чисел в Rust. ## Числа с плавающей точкой Исторически сложилось, что в компьютерной технике вещественные числа представляются в виде чисел с [плавающей точкой (floating point)](https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%BE_%D1%81_%D0%BF%D0%BB%D0%B0%D0%B2%D0%B0%D1%8E%D1%89%D0%B5%D0%B9_%D0%B7%D0%B0%D0%BF%D1%8F%D1%82%D0%BE%D0%B9). Числа с плавающей точкой являются компромиссом между точностью и диапазоном принимаемых значений. В Rust числа с плавающей точкой представлены двумя типами: `f32` и `f64`. Дробные значения задаются в десятичной и [экспоненциальной](https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D1%8C) записях. С помощью суффиксов `f32` и `f64` можно указать тип литерала: ```rust {.example_for_playground .example_for_playground_001} use std::any::type_name_of_val as tn; let single = 90000.1234567894444_f32; let double = 90000.1234567894444_f64; let default = 90000.1234567894444; println!("single: {} = {}", tn(&single), single); println!("double: {} = {}", tn(&double), double); println!("default: {} = {}", tn(&default), default); ``` В консоль будет выведено: ``` single: f32 = 90000.125 double: f64 = 90000.12345678944 default: f64 = 90000.12345678944 ``` Если тип литерала числа с плавающей точкой не указан, то по умолчанию используется тип `f64`. Представление литералов вещественных чисел в системе отличной от десятичной невозможно. Значение `single` было округлено до тысячных, а значение переменных `double` и `default` до `10` в степени `-12`. Допустимо задать значение вещественного числа в экспоненциальной форме. А с помощью спецификации формата `{:e}` можно вывести число в экспоненциальной форме: ```rust {.example_for_playground .example_for_playground_002} let sun = 1.98847e30_f64; let milky_way = sun * 2e12; println!("mass of Sun: {} kg", sun); println!("mass of Milky Way: {:e} kg", milky_way); ``` Масса Земли будет представлена в десятичной записи, масса Млечного пути — в экспоненциальной форме: ``` mass of Sun: 1988470000000000000000000000000 kg mass of Milky Way: 3.97694e42 kg ``` Над числами с плавающей точкой возможны операции: - арифметические: `+`, `-`, `*`, `/`, `%`; - сравнения: `==`, `!=`, `>`, `>=`, `<`, `<=`. Подробнее сравнение на равенство чисел с плавающей точкой будет рассмотрено [другом разделе](/courses/rust/chapters/rust_chapter_0080#block-floating-point-comparision) этой главы. Формула преобразования температуры из градусов Цельсия (°C) в градусы Фаренгейта (°F): `°F = 1.8 * °C + 32`. Необходимо реализовать функции `to_fahrenheit()` и `to_celsius()`, преобразующие градусы из одной шкалы в другую. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0010} fn to_fahrenheit(celsius: f64) -> f64 { // добавьте реализацию функции } fn to_celsius(fahrenheit: f64) -> f64 { // добавьте реализацию функции } ``` Формула преобразования из градусов в Цельсий: `°C = (°F - 32) * 5 / 9`. При задании литералов вещественных чисел следует указывать дробную часть, например `5.0`, либо суффикс, например `9f64`. {.task_hint} ```rust {.task_answer} fn to_fahrenheit(celsius: f64) -> f64 { 1.8 * celsius + 32.0 } fn to_celsius(fahrenheit: f64) -> f64 { (fahrenheit - 32.0) / 9.0 * 5.0 } ``` ## Нечисловые значения вещественных чисел Для чисел с плавающей точкой есть специальные значения: нечисло (_Not-a-Number, NaN_) и бесконечность (_Infinity_). Нечисло возникает в математической операции с неопределенным результатом: ```rust {.example_for_playground .example_for_playground_003} // деление 0 на 0 println!("0 / 0 = {}", 0.0 / 0.0); // деление бесконечность на бесконечность println!("∞ / ∞ = {}", f64::INFINITY / f64::INFINITY); // умножение бесконечность на 0 println!("∞ * 0 = {}", f32::INFINITY * 0.0); // бесконечность минус бесконечность println!("∞ - ∞ = {}", f32::INFINITY - f32::INFINITY); // квадратный корень из отрицательного числа println!("-4.sqrt() = {}", (-4_f32).sqrt()); // логарифм отрицательного числа println!("-16.log() = {}", (-16_f64).log(2.0)); // логарифм c отрицательным основанием println!("16.log(-2) = {}", 16_f64.log(-2.0)); // операция, в которой хотя бы один параметр NaN println!("7 + NaN = {}", 7_f32 + f32::NAN); ``` Вывод: ``` 0 / 0 = NaN ∞ / ∞ = NaN ∞ * 0 = NaN ∞ - ∞ = NaN -4.sqrt() = NaN -16.log() = NaN 16.log(-2) = NaN 7 + NaN = NaN ``` Нечисло не равно ни одному другому значению (даже самому себе). Нечисло представлено константами: `f32::NAN` `f64::NAN`. Для определения нечисла используется метод `is_nan()`. Бесконечность бывает положительная и отрицательная. Бесконечность может быть получена в результате таких математических операций: ```rust {.example_for_playground .example_for_playground_004} // деление на ноль println!("9 / 0 = {}", 9.0 / 0.0); // при переполнении println!("f64::MAX + 2e292 = {}", f64::MAX + 2e292); println!("f32::MIN * 1.1 = {}", f32::MIN * 1.1); println!("10.pow(309) = {}", 10_f64.powf(309.0)); println!("f64::MAX as f32 = {}", f64::MAX as f32); // операция, в которой хотя бы один параметр ∞ // за исключением случаев приводящих к NaN println!("-∞ + 51e30 = {}", f32::NEG_INFINITY + 51e30); ``` Вывод: ``` 9 / 0 = inf f64::MAX + 2e292 = inf f32::MIN * 1.1 = -inf 10.pow(309) = inf f64::MAX as f32 = inf -∞ + 51e30 = -inf ``` Положительная бесконечность больше любого числа с плавающей точкой, отрицательная — меньше любого. Бесконечность представлена константами: `f32::NEG_INFINITY`, `f32::INFINITY` и `f64::NEG_INFINITY`, `f64::INFINITY`. Для определения бесконечности используется метод `is_infinite()`. Метод `is_finite()` проверяет, что значение является конечным действительным числом, то есть не является ни бесконечным, ни нечислом. ``` 2.7.is_finite() -> true NaN.is_finite() -> false inf.is_finite() -> false ``` Необходимо реализовать функцию `clamp()`, которая ограничивает значение `val` заданным интервалом `[min, max]`. Функция возвращает: {.task_text} - `min`, если `val` меньше минимального значения интервала; - `max`, если `val` больше максимального значения интервала; - `nan`, если `val` — нечисло. {.task_text} В других случаях `clamp()` возвращает значение `val`. Гарантируется, что `min` не превышает `max` и оба параметра не могут быть нечислом. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0020} fn clamp(val: f64, min: f64, max: f64, nan: f64) -> f64 { // добавьте реализацию функции } ``` С помощью метода `is_nan()` можно проверить, является ли `val` нечислом. {.task_hint} ```rust {.task_answer} fn clamp(val: f64, min: f64, max: f64, nan: f64) -> f64 { if val.is_nan() { nan } else if val < min { min } else if val > max { max } else { val } } ``` ## Методы чисел с плавающей точкой У чисел с плавающей точкой `f32` и `f64` есть множество полезных методов: округление до целого, возведение в степень, экспоненциальные, логарифмические, тригонометрические и другие функции. Ниже приведены некоторые из них. Округление до целого: ```rust {.example_for_playground .example_for_playground_005} let values = vec![4.49_f32, 4.5_f32, 5.5_f32]; println!("Округление до ближайшего целого:"); for val in &values { println!("{}.round() -> {}", val, val.round()); } let values = vec![1_f32 - f32::EPSILON, 4.5_f32, -4.5_f32]; println!("\nНаибольшее целое, меньшее или равное дробному:"); for val in &values { println!("{}.floor() -> {}", val, val.floor()); } println!("\nОтбрасывание дробной части:"); for val in &values { println!("{}.trunc() -> {}", val, val.trunc()); } ``` ``` Округление до ближайшего целого: 4.49.round() -> 4 4.5.round() -> 5 5.5.round() -> 6 Наибольшее целое, меньшее или равное дробному: 0.9999999.floor() -> 0 4.5.floor() -> 4 -4.5.floor() -> -5 Отбрасывание дробной части: 0.9999999.trunc() -> 0 4.5.trunc() -> 4 -4.5.trunc() -> -4 ``` Операции со знаком: ```rust {.example_for_playground .example_for_playground_006} let values = vec![9.3_f64, -9.3_f64, f64::NEG_INFINITY]; println!("Модуль числа:"); for val in &values { println!("{}.abs() -> {}", val, val.abs()); } println!("\nПроверка знака числа:"); for val in &values { println!("{}.is_sign_positive() -> {}", val, val.is_sign_positive()); println!("{}.is_sign_negative() -> {}\n", val, val.is_sign_negative()); } ``` ``` Модуль числа: 9.3.abs() -> 9.3 -9.3.abs() -> 9.3 -inf.abs() -> inf Проверка знака числа: 9.3.is_sign_positive() -> true 9.3.is_sign_negative() -> false -9.3.is_sign_positive() -> false -9.3.is_sign_negative() -> true -inf.is_sign_positive() -> false -inf.is_sign_negative() -> true ``` Возведение в степень и вычисление корня: ```rust {.example_for_playground .example_for_playground_007} let val = 2_f32; let pow = 6_i32; let res = val.powi(pow); println!("Возведение в степень:"); println!("{}.powi({}) -> {}", val, pow, res); let pow = 0.5_f32; println!("{}.powf({}) -> {}", res, pow, res.powf(pow)); println!("\nКвадратный корень:"); println!("{}.sqrt() -> {}", res, res.sqrt()); println!("\nКубический корень:"); println!("{}.cbrt() -> {}", res, res.cbrt()); ``` ``` Возведение в степень: 2.powi(6) -> 64 64.powf(0.5) -> 8 Квадратный корень: 64.sqrt() -> 8 Кубический корень: 64.cbrt() -> 4 ``` Экспоненциальные и логарифмические функции: ```rust {.example_for_playground .example_for_playground_008} println!("Экпонента:"); let val = 4_f64; let exp = val.exp(); println!("{}.exp() -> {}", val, exp); println!("Натуральный логарифм:"); println!("{}.ln() -> {}", exp, exp.ln()); println!("\nВозведение 2 в степень:"); let val2 = 10_f64; let exp2 = val2.exp2(); println!("{}.exp2() -> {}", val2, exp2); println!("Двоичный логарифм:"); println!("{}.log2() -> {}", exp2, exp2.log2()); ``` ``` Экпонента: 4.exp() -> 54.598150033144236 Натуральный логарифм: 54.598150033144236.ln() -> 4 Возведение 2 в степень: 10.exp2() -> 1024 Двоичный логарифм: 1024.log2() -> 10 ``` Получение битового образа и преобразование порядка следования байтов: ```rust {.example_for_playground .example_for_playground_009} println!("Битовый образ:"); let val = 3087.125_f32; let bits = val.to_bits(); println!("{}.to_bits() -> {:b}", val, bits); println!("from_bits({:b}) -> {}", bits, f32::from_bits(bits)); println!("\nПорядок следования байтов:"); let be_bytes = val.to_be_bytes(); let le_bytes = val.to_le_bytes(); println!("{}.to_be_bytes() -> {:?}", val, be_bytes); println!("{}.to_le_bytes() -> {:?}", val, le_bytes); println!("\nfrom_be_bytes({:?}) -> {}", be_bytes, f32::from_be_bytes(be_bytes)); println!("from_le_bytes({:?}) -> {}", le_bytes, f32::from_le_bytes(le_bytes)); ``` ``` Битовый образ: 3087.125.to_bits() -> 1000101010000001111001000000000 from_bits(1000101010000001111001000000000) -> 3087.125 Порядок следования байтов: 3087.125.to_be_bytes() -> [69, 64, 242, 0] 3087.125.to_le_bytes() -> [0, 242, 64, 69] from_be_bytes([69, 64, 242, 0]) -> 3087.125 from_le_bytes([0, 242, 64, 69]) -> 3087.125 ``` Полный список методов можно посмотреть в официальной документации [f32](https://doc.rust-lang.org/std/primitive.f32.html) и [f64](https://doc.rust-lang.org/std/primitive.f64.html). [Среднее квадратическое](https://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D0%B5_%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5) — это квадратный корень из среднего арифметического квадратов чисел массива. Необходимо реализовать функцию `rms()`, вычисляющую среднее квадратическое (root mean square) для заданного массива. Гарантируется, что массив будет не пустым, а его элементы больше либо равны `0`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0030} fn rms(numbers: &[f32]) -> f32 { // добавьте реализацию функции } ``` Для обхода массива лучше воспользоваться циклом `for`. Получить количество элементов массива можно с помощью метода `len()`. Полученное количество элементов потребуется преобразовать в `f32` с помощью ключевого слова `as`. {.task_hint} ```rust {.task_answer} fn rms(numbers: &[f32]) -> f32 { let mut res = 0.0_f32; for num in numbers { res += num.powi(2); } (res / numbers.len() as f32).sqrt() } ``` В следующих разделах рассказывается о представлении чисел с плавающей точкой в памяти компьютера, о проблемах с точностью вычислений и о корректном сравнении таких чисел. ## Представление чисел с плавающей точкой в памяти В памяти число с плавающей точкой представляется в виде двоичной дроби в [экспоненциальной записи](https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D1%8C) в нормализованной форме: `m * 2 ** k`, где `m` — значащая часть (мантисса), `2 ** k` — порядок (`2` в степени `k`). Нормализованная форма означает, что мантисса по модулю больше либо равна 1 и меньше 2: `1 <= |m| < 2` (исключением является `0`). Хранение чисел с плавающей точкой основано на стандарте [IEEE 754-2008](https://ru.wikipedia.org/wiki/IEEE_754-2008). Тип `f32` соответствует стандарту ([одинарной точности](https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%BE_%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D1%80%D0%BD%D0%BE%D0%B9_%D1%82%D0%BE%D1%87%D0%BD%D0%BE%D1%81%D1%82%D0%B8)), a `f64` — ([двойной точности](https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%BE_%D0%B4%D0%B2%D0%BE%D0%B9%D0%BD%D0%BE%D0%B9_%D1%82%D0%BE%D1%87%D0%BD%D0%BE%D1%81%D1%82%D0%B8)). 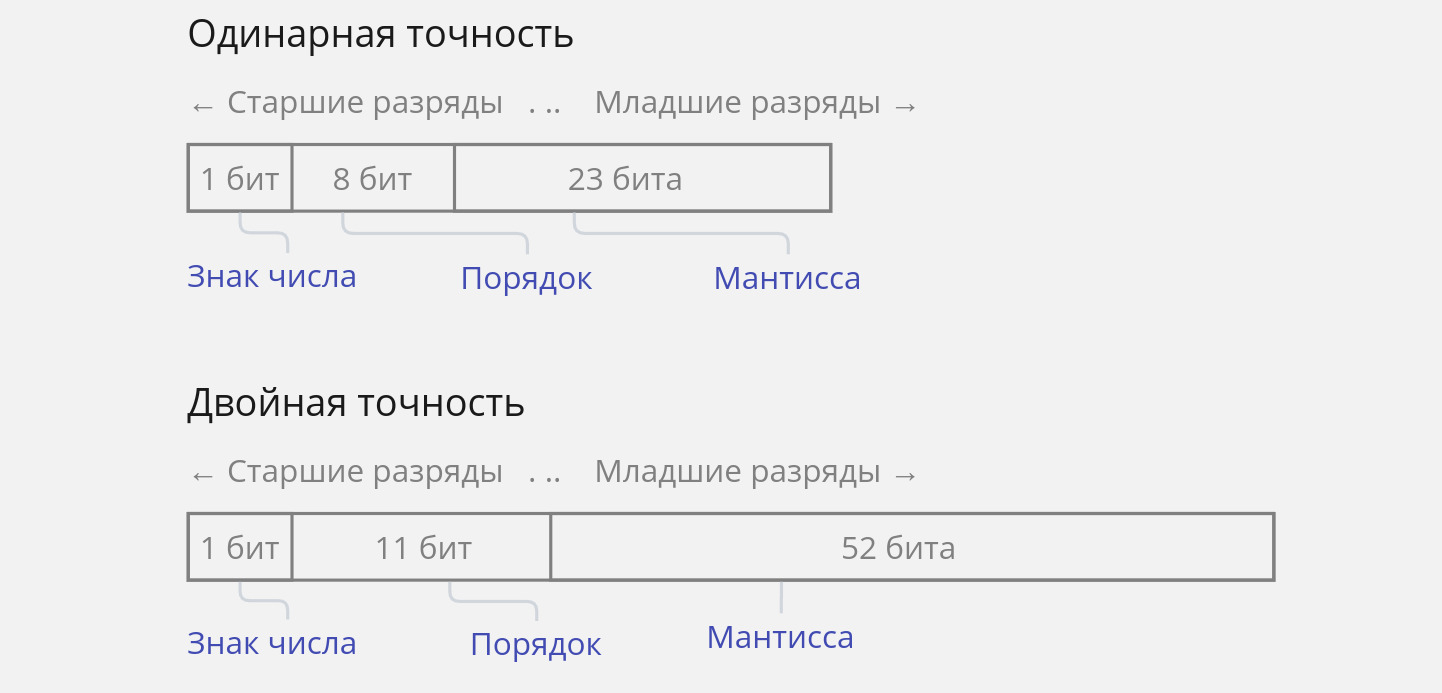 {.illustration} Бит знака принимает значение `0` для положительных чисел и `1` для отрицательных. Так как в нормализованном двоичном представлении целая часть мантиссы всегда равна `1`, то в поле мантиссы записывается только ее дробная часть. Поэтому для вычисления значения мантиссы к `1` добавляется дробная часть из поля мантиссы. Величина показателя степени смещена наполовину относительно возможного значения. Это означает, что при вычислении показателя степени из поля вычитается смещение, равное `127` для `f32` и `1023` для `f64`. Функция `explore()` печатает битовое представление числа c плавающей точкой одинарной точности: ```rust {.example_for_playground .example_for_playground_010} fn explore(float: f32) { const SIGN_SHIFT: u32 = 31; const EXP_SHIFT: u32 = 23; const EXP_BITS: u32 = 0xFF; const MANTISSA_BITS: u32 = 0x7FFFFF; let float_bits = float.to_bits(); // выделение знака числа let sign = float_bits >> SIGN_SHIFT; // выделение показателя степени let exp = (float_bits >> EXP_SHIFT) & EXP_BITS; // выделение мантиссы let mantissa = float_bits & MANTISSA_BITS; println!("Представление в памяти числа {}:", float); println!("┌─ ┌───────────────────────"); println!("│знак │мантисса"); println!("│{:b}│{:0>8b}│{:0>23b}│", sign, exp, mantissa); println!(" │показатель степени"); println!(" └────────"); } ``` Для числа `18.5` будет напечатано: ``` Представление в памяти числа 18.5: ┌─ ┌─────────────────────── │знак │мантисса │0│10000011│00101000000000000000000│ │показатель степени └──────── ``` По битовому представлению можно вычислить значение числа с плавающей точкой. Бит знака равен `0`, значит число положительное. Для вычисления значения мантиссы нужно к целой части добавить дробную из одноименного поля. То есть к `1` добавляется дробное значение `00101` (незначащие нули опущены). Таким образом значение мантиссы равно `1.00101`. Показатель степени вычисляется как значение соответствующего поля минус `127`: `10000011 - 01111111 = 100`. Теперь можно запиcать полученные значения мантиссы и степени в экспоненциальной форме: ``` 1.00101 * 10 ** 100 = (100101 / 100000) * 10000 = 100101 / 10 ``` Выражение `100101 / 10` в десятичной системе счисления будет соответствовать `37 / 2`, то есть `18.5`. Из-за особенности компоновки чисел в стандарте [IEEE 754-2008](https://ru.wikipedia.org/wiki/IEEE_754-2008) существует два нуля, отрицательный и положительный: ``` 0_f32: 0 00000000 00000000000000000000000 -0_f32: 1 00000000 00000000000000000000000 ``` Несмотря на разное значение старшего бита эти значения равны между собой: ```rust {.example_for_playground .example_for_playground_011} if 0.0 == -0.0 { println!("0.0 == -0.0"); } ``` Этот код выведет: `0.0 == -0.0`. Преимуществом чисел с плавающей точкой перед числами с [фиксированной точкой (fixed-point)](https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%BE_%D1%81_%D1%84%D0%B8%D0%BA%D1%81%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%BE%D0%B9_%D0%B7%D0%B0%D0%BF%D1%8F%D1%82%D0%BE%D0%B9) является существенно больший диапазон значений: ```rust {.example_for_playground .example_for_playground_012} println!("f32: [{:e}, {:e}]", f32::MIN, f32::MAX); println!("f64: [{:e}, {:e}]", f64::MIN, f64::MAX); ``` Вывод: ``` f32: [-3.4028235e38, 3.4028235e38] f64: [-1.7976931348623157e308, 1.7976931348623157e308] ``` Числа представленные в формате [IEEE 754-2008](https://ru.wikipedia.org/wiki/IEEE_754-2008) образует конечное множество, на которое отображается бесконечное множество вещественных чисел. Поэтому не каждое вещественное число может быть представлено в формате IEEE 754-2008 без погрешности. Другой неприятной особенностью является изменяющаяся абсолютная точность представления чисел в IEEE 754-2008 (при постоянной относительной точности). Так для сетки чисел с одинарной точностью за `1.0` следует число `1.00000011920929`, в памяти они представлены как: ``` 0 01111111 00000000000000000000000 0 01111111 00000000000000000000001 ``` Дельта между ними составляет `1.1920929e-7`, эта величина называется [машинным эпсилоном](https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BD%D0%BE%D0%BB%D1%8C) и соответствует константе `f32::EPSILON`. Ближайшим меньшим числом к `3.4028235e38 (f32::MAX)` будет значение `3.4028233e38`: ``` 0 11111110 11111111111111111111111 0 11111110 11111111111111111111110 ``` Дельта между ними равна значению `2.028241e31`. Ожидаемо, что с ростом порядка дельта между соседними числами растет, а точность падает. В отличие от чисел с фиксированной точкой, сетка чисел с плавающей точкой неравномерна: она более густая для чисел с малыми порядками и более редкая для чисел с большими порядками. Поэтому погрешность вычислений для чисел в интервале `(1f32, 2f32)` равна `0.00000011920929 (f32::EPSILON)`, а для а для интервала `(1.7014118e38f32, 3.4028235e38f32]` составляет уже `20282410000000000000000000000000` — [20.28241 нониллиона](https://ru.wikipedia.org/wiki/%D0%98%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D0%B5_%D0%BD%D0%B0%D0%B7%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D1%81%D1%82%D0%B5%D0%BF%D0%B5%D0%BD%D0%B5%D0%B9_%D1%82%D1%8B%D1%81%D1%8F%D1%87%D0%B8). Функция `is_integer()` определяет является ли число с плавающей точкой целым. На вход функция получает битовый образ числа типа `f32`. Функция возвращает `true`, если заданное число целое, в противном случае — `false`. Необходимо реализовать `is_integer()`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0040} fn is_integer(float_bits: u32) -> bool { // добавьте реализацию функции } ``` Перед решением задачи стоит учесть, что умножение числа на `2` в степени `N` аналогично битовому сдвигу влево на `N`. Необходимо вычислить значение показателя степени и мантиссу. Если значение показателя степени меньше `127`, то единственное целоe в этом диапазоне — `0`, мантисса которого также равна нулю. Если значение показателя степени больше либо равно 127 + 23 (количество бит в мантиссе), то такое число заведомо целое. Если значение показателя степени находится в диапазоне `[127, 150)`, то следует отнять от него `127`. Полученное значение использовать для сдвига мантиссы влево. После сдвига правые `23` бита мантиссы будут содержать дробную часть. Если дробная часть равна `0`, то число целое. {.task_hint} ```rust {.task_answer} fn is_integer(float_bits: u32) -> bool { const HALF_EXP: u32 = 127; const EXP_BITS: u32 = 0xFF; const MANTISSA_BITS: u32 = 0x7FFFFF; const MANTISSA_BITS_COUNT: u32 = 23; let exp = (float_bits >> MANTISSA_BITS_COUNT) & EXP_BITS; let mantissa = float_bits & MANTISSA_BITS; if exp < HALF_EXP { mantissa == 0 } else if exp >= HALF_EXP + MANTISSA_BITS_COUNT { true } else { let exp = exp - HALF_EXP; let fractional = (mantissa << exp) & MANTISSA_BITS; fractional == 0 } } ``` ## Особенности обработки чисел с плавающей точкой Проблемы с точностью чисел в формате IEEE 754-2008 могут приводить к неожиданным результатам: ```rust {.example_for_playground .example_for_playground_013} let a = 123456789_f32; let b = 123456788_f32; let c = a - b; println!("a: {:.2}", a); println!("b: {:.2}", b); println!("c: {:.2}", c); ``` Может показаться, что после выполнения кода переменная `c` будет содержать `1`, но это не так: ``` a: 123456792.00 b: 123456784.00 c: 8.00 ``` Отображение исходных чисел в `f32` произошло с погрешностью: `123456789` ==> `123456792`, `123456788` ==> `123456784`. Разница между фактическими значениями оказалась равна `8`. Также проблема возникает при сложении/вычитании чисел с разными порядками. Если к числу с большим порядком прибавить число значительно меньшее, то оно может быть проигнорированно: ```rust {.example_for_playground .example_for_playground_014} let big = 27108871847099104_f64; let small = 2.0_f64; let sum = big + small; println!("{}", sum); ``` Программа выведет значение переменной `big`, то есть `27108871847099104`. Если представить это число в экспоненциальной форме степени двух, то получится `1.5048446848131060704645278747193515300750732421875 * 2 ** 54`. Число `2` в экспоненциальной форме — `1.0 * 2 ** 1`. Разница между показателями степени чисел равна `53`, а длина мантиссы `f64` составляет `52` бита. Таким образом мантисса числа `2` не пересекается с мантиссой `27108871847099104`. Если числа отличаются более чем в `2 ** 23` (для `f32`) и `2 ** 52` (для `f64`), то операции сложения и вычитания между этими числами бессмыслены. Одиночное сложение большого дробного числа с малым — не проблема. Проблема возникает, когда подобное сложение повторяется множество раз. Например, в цикле при многократном сложении малых чисел c большим: ```rust {.example_for_playground .example_for_playground_015} const COUNT: i64 = 1_000_000_000; fn sum(big: f64, small: f64) -> f64 { let mut sum = big; for _i in 0..COUNT { sum += small; } sum } ``` В цикле функция `sum()` миллиард раз добавляет `small` к `big`. Для значений `1e16` и `1.0` функция вернет: ``` sum(1e16, 1.0) -> 10000000000000000 ожидаемое значение: 10000001000000000 абсолютная погрешность: 1000000000 ``` Миллиард добавлений `1.0` прошел бесследно. Если заменить значение `small` на `3.0`, то результирующее значение будет на миллиард больше: ``` sum(1e16, 3.0) -> 10000004000000000 ожидаемое значение: 10000003000000000 абсолютная погрешность: 1000000000 ``` Несмотря на большую абсолютную погрешность относительная погрешность невелика и равна примерно `0.00001%`. В ряде задач такой погрешностью можно пренебречь. Но для некоторых задач такая погрешность недопустима, например, в финансах. Проблему сложения малых чисел с большим можно решить, введя поправочное значение: ```rust {.example_for_playground .example_for_playground_016} const COUNT: i64 = 1_000_000_000; fn sum(big: f64, small: f64) -> f64 { let mut sum = big; let mut fix: f64 = 0.0; // (1) for _i in 0..COUNT { let prev = sum; // (2) sum += small + fix; // (3) let diff = sum - prev; // (4) fix += small - diff; // (5) } sum } ``` (1) Начальное значение поправки `0.0`. (2) Сохранение текущего значения суммы. (3) Добавление к сумме малого значения с поправкой. (4) Вычисление разницы между текущим и прежним значениями суммы. (5) Вычисление нового значения поправки: - если сумма не изменилась, то поправка увеличится на значение `small`; - если сумма увеличилась на полное значение `small + fix`, то поправка обнулится; - если сумма увеличилась на иное значение, то поправка скорректируется в большую или меньшую сторону. С помощью такого подхода можно получать более точные результаты: ``` sum(1e16, 1.0) -> 10000001000000000 ожидаемое значение: 10000001000000000 абсолютная погрешность: 0 sum(1e16, 3.0) -> 10000003000000000 ожидаемое значение: 10000003000000000 абсолютная погрешность: 0 ``` Фармацевтический цех производит антибиотики в таблетках. Цех состоит из: формовочной машины, накопительной камеры на 600 кг, фасовочной машины и автоматической системы управления. Формовочная машина подает в накопительную камеру таблетки, а фасовочная машина их забирает по одной. {.task_text} Автоматическая система управления контролирует подачу и забор таблеток из камеры с учетом веса накопленной продукции. Забор таблеток останавливается по сигналу датчика. Датчик срабатывает, если в накопительной камере осталось мало продукции или поступил внешний сигнал остановки. {.task_text} Алгоритм подсчета веса продукции в накопительной камере во время расфасовки реализован в функции `packing()`. На вход функция принимает: `storage` — вес продукции в накопительной камере на начало расфасовки, `probe` — датчик с методами `collect()` и `last_collected()`. Метод `collect()` возвращает `false`, если расфасовку нужно остановить. Вызов метода `collect()` соответствует одному отбору таблеток из камеры. За раз может быть отобрано от одной до нескольких таблеток. Метод `last_collected()` возвращает вес отобранных таблеток в последний раз. {.task_text} Функция работает некорректно, вес вычисляется с существенными погрешностями. Необходимо исправить реализацию функции `packing()`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0050} fn packing(storage: f32, probe: &mut control::Probe) -> f32 { let mut remains = storage; while probe.collect(remains) { remains -= probe.last_collected(); } remains } ``` Нужно ввести поправку и использовать ее при вычислении веса оставшейся продукции. Начальное значение поправки 0. Поправка вычисляется на каждой итерации цикла. Алгоритм: 1) сохранить текущий вес продукции; 2) вычислить новый вес продукции, вычтя из текущего вес отобранных таблеток и поправки; 3) вычислить расхождение между новым и прежним весами продукции; 4) увеличить поправку на разницу между весом отобранных таблеток и расхождением, вычисленным на предыдущем шаге. {.task_hint} ```rust {.task_answer} fn packing(storage: f32, probe: &mut control::Probe) -> f32 { let mut remains = storage; let mut fix: f32 = 0.0; while probe.collect(remains) { let picked = probe.last_collected(); let prev = remains; remains -= picked + fix; let diff = prev - remains; fix += picked - diff; } remains } ``` ## Алгоритмы сравнения чисел с плавающей точкой {#block-floating-point-comparision} Не каждое вещественное число может быть точно представлено в виде числа с плавающей точкой. Кроме того, число конечное в десятичном представлении может оказаться бесконечным в двоичном представлении. Поэтому точное сравнение чисел с плавающей точкой зачастую не работает как ожидается. Пример: ```rust {.example_for_playground .example_for_playground_017} let sum: f64 = 0.1 + 0.2; if sum == 0.3 { println!("{} == {}", sum, 0.3); } else { println!("{} != {}", sum, 0.3); } ``` Вместо ожидаемого `0.3 == 0.3` программа напечатает `0.30000000000000004 != 0.3`. Проблема в том, что ни одно из реальных значений в формате IEEE 754-2008 не равно заданным действительным числам. Чтобы убедиться в этом, достаточно распечатать значения с точностью до 20 знака после точки: ```rust {.example_for_playground .example_for_playground_018} let sum: f64 = 0.1 + 0.2; println!("0.1: {:.20}", 0.1); println!("0.2: {:.20}", 0.2); println!("sum: {:.20}", sum); println!("0.3: {:.20}", 0.3); ``` На экран будет выведено: ``` 0.1: 0.10000000000000000555 0.2: 0.20000000000000001110 sum: 0.30000000000000004441 0.3: 0.29999999999999998890 ``` ### Cравнение с абсолютным эпсилон Проблема сравнения двух чисел с плавающей точкой не так проста, как может показаться на первый взгляд. Наиболее очевидное решение — сравнение с абсолютной погрешностью `ε` (эпсилон). Суть идеи в том, чтобы проверить, находится ли разница двух вещественных чисел в пределах заданного эпсилон. Функция `approx_equal_abs()` проверяет два числа на равенство в пределах заданного эпсилон. Функция возвращает `true`, если разность сравниваемых чисел по модулю не превышает эпсилон, в противном случае — `false`. Необходимо реализовать `approx_equal_abs()`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0060} fn approx_equal_abs(left: f64, right: f64, epsilon: f64) -> bool { // добавьте реализацию функции } ``` При вычислении разницы следует вычитать из большего меньшее либо брать модуль с помощью метода `abs()`. В начале следует проверить числа на точное равенство, это требуется для случая сравнения двух бесконечностей. {.task_hint} ```rust {.task_answer} fn approx_equal_abs(left: f64, right: f64, epsilon: f64) -> bool { left == right || (left - right).abs() <= epsilon } ``` Cравнение с абсолютным эпсилон хорошо работает при правильно подобранном эпсилон. Это несложно, когда заранее известен порядок сравниваемых вещественных чисел: ```rust {.example_for_playground .example_for_playground_019} let sum: f64 = 0.1 + 0.2; if approx_equal_abs(sum, 0.3, 0.01) { println!("{} == {} with epsilon {}", sum, 0.3, 0.01); } if approx_equal_abs(sum, 0.31, 0.01) { println!("{} == {} with epsilon {}", sum, 0.31, 0.01); } if !approx_equal_abs(sum, 0.311, 0.01) { println!("{} != {} with epsilon {}", sum, 0.311, 0.01); } ``` Вывод: ``` 0.30000000000000004 == 0.3 with epsilon 0.01 0.30000000000000004 == 0.31 with epsilon 0.01 0.30000000000000004 != 0.311 with epsilon 0.01 ``` Cравнение с абсолютным эпсилон довольно часто будет истинным для чисел, модуль которых меньше эпсилон. И это ожидаемое поведение: ```rust {.example_for_playground .example_for_playground_020} // сравнение с абсолютным epsilon еще работает assert!(!approx_equal_abs(0.0055, -0.005, 0.01)); println!("{} != {} with epsilon {}", 0.0055, -0.005, 0.01); // уже не работает assert!(approx_equal_abs(0.005, -0.005, 0.01)); println!("{} == {} with epsilon {}", 0.005, -0.005, 0.01); assert!(approx_equal_abs(0.009, 9e-300, 0.01)); println!("{:e} == {:e} with epsilon {}", 0.009, 9e-300, 0.01); ``` Вывод: ``` 0.0055 != -0.005 with epsilon 0.01 0.005 == -0.005 with epsilon 0.01 9e-3 == 9e-300 with epsilon 0.01 ``` Для чисел с дельтой больше эпсилон подобное сравнение всегда будет ложным. В примере сравниваются два дробных числа, стоящих рядом в сетке чисел двойной точности (`f64`), ближе некуда. Дельта между ними равна `0.015625`, что больше `ε = 0.01`: ```rust {.example_for_playground .example_for_playground_021} let left = 100000000000000.0_f64; let right = 100000000000000.015625_f64; assert!(!approx_equal_abs(left, right, 0.01)); println!("{} != {:.6} with epsilon {}", left, right, 0.01); println!("left: 0x{:X}", left.to_bits()); println!("right: 0x{:X}", right.to_bits()); ``` О близости чисел можно судить по их битовым представлениям. Для получения битового образа используется метод `to_bits()`. Выбранные числа отличаются только значением младшего бита: ``` 100000000000000 != 100000000000000.015625 with epsilon 0.01 left: 0x42D6BCC41E900000 right: 0x42D6BCC41E900001 ``` ### Сравнение с относительным эпсилон Если заранее неизвестен порядок сравниваемых дробных чисел, то можно воспользоваться алгоритмом сравнения c относительной погрешностью `ε` (эпсилон). Идея заключается в том, чтобы найти разницу между двумя вещественными числами и посмотреть, насколько она мала по сравнению с их величинами. То есть нужно сравнить модуль разницы двух чисел с наибольшим по модулю числом умноженным на эпсилон. Вот как это может выглядеть в коде: ```rust {.example_for_playground .example_for_playground_022} fn approx_equal_rel(left: f64, right: f64, epsilon: f64) -> bool { left == right || { let max = left.abs().max(right.abs()); (left - right).abs() <= max * epsilon } } ``` Для случаев, в которых алгоритм сравнения с эпсилон пасует, алгоритм сравнения с относительным эпсилон работает: ``` 0.005 != -0.005 with epsilon 0.01 9e-3 != 9e-300 with epsilon 0.01 100000000000000 == 100000000000000.015625 with epsilon 0.01 ``` В целом алгоритм с относительным эпсилон работает хорошо, но не всегда очевиден результат сравнения. Например, числа `0.31` и `0.306` выглядят достаточно близкими для `ε = 0.01`: ```rust {.example_for_playground .example_for_playground_023} assert!(!approx_equal_rel(0.31, 0.306, 0.01)); println!("{} != {} with epsilon {}", 0.31, 0.306, 0.01); ``` Однако они не равны: ``` 0.31 != 0.306 with epsilon 0.01 ``` Разница между числам составляет: `0.31 - 0.306 = 0.0040000000000000036`. А относительный эпсилон умноженный на масимальное значение из пары равен: `0.31 * 0.01 = 0.0031`. То есть разница оказалась больше: `0.004 > 0.0031`. Алгоритм с относительным эпсилон плохо работает с числами близкими к нулю. Например, если сравнить минимальное положительное число с плавающей точкой `5e-324` с `0.0`: ```rust {.example_for_playground .example_for_playground_024} assert!(!approx_equal_rel(5e-324, 0.0, 0.01)); println!("{:e} != {} with epsilon {}\n", 5e-324, 0.0, 0.01); println!("5e-324.to_bits() -> {}", 5e-324_f64.to_bits()); println!("0.to_bits() -> {}", 0.0_f64.to_bits()); ``` Результат будет негативным, несмотря на то, что числа рядом стоящие: ``` 5e-324 != 0 with epsilon 0.01 5e-324.to_bits() -> 1 0.to_bits() -> 0 ``` Для контроля воздуха в чистой зоне производства электронных компонент используются датчики атмосферной взвеси **PM2.5**. В чистой зоне установлено три таких датчика. Показание датчика считается достоверным, если есть показание другого датчика, равное этому. Сравнение производится с заданным относительным эпсилон. Бесконечность и нечисло являются некорректными значениями датчиков. Если нет хотя бы одной пары равных значений, то все показания датчиков считаются некорректными. {.task_text} Функция `analyze()` получает показания датчиков в параметрах: `probe_1`, `probe_2` и `probe_3`. Относительный эпсилон передается в параметре `epsilon`. Функция вычисляет среднее арифметическое корректных значений датчиков. Если корректных показаний нет, то функция возвращает `f64::NAN`. Необходимо реализовать функцию `analyze()`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0070} fn analyze(probe_1: f64, probe_2: f64, probe_3: f64, epsilon: f64) -> f64 { // добавьте реализацию функции } ``` Для решения задачи также потребуется реализовать функцию сравнения с относительным эпсилон. Функция сравнения должна учитывать, что оба значения не являются ни бесконечностью, ни NaN. С помощью функции сравнения нужно найти пары одинаковых значений. Если таких пары две или три, то все показания датчиков корректные. Если одна пара — только два показания корректны. При вычислении среднего арифметического нужно учитывать только корректные значения и их число. {.task_hint} ```rust {.task_answer} fn approx_equal_rel(left: f64, right: f64, epsilon: f64) -> bool { left.is_finite() && right.is_finite() && (left == right || { let max = left.abs().max(right.abs()); (left - right).abs() <= max * epsilon }) } fn analyze(probe_1: f64, probe_2: f64, probe_3: f64, epsilon: f64) -> f64 { let equal_1_2 = approx_equal_rel(probe_1, probe_2, epsilon); let equal_1_3 = approx_equal_rel(probe_1, probe_3, epsilon); let equal_2_3 = approx_equal_rel(probe_2, probe_3, epsilon); if equal_1_2 && equal_1_3 || equal_1_2 && equal_2_3 || equal_1_3 && equal_2_3 { (probe_1 + probe_2 + probe_3) / 3.0 } else if equal_1_2 { (probe_1 + probe_2) / 2.0 } else if equal_1_3 { (probe_1 + probe_3) / 2.0 } else if equal_2_3 { (probe_2 + probe_3) / 2.0 } else { f64::NAN } } ``` ### ULP cравнение Соседние числа с плавающей точкой одинакового знака имеют смежные битовые представления. Если вычислить разность битовых представлений таких чисел, то абсолютное значение результата будет равно количеству представимых чисел с плавающей точкой между ними плюс один. Этот метод называется ULP сравнением (Unit in the Last Place comparsion). Он позволяет определить насколько два числа с плавающей точкой близки друг к другу. Возможная реализация: ```rust {.example_for_playground .example_for_playground_025} fn approx_equal_ulp(left: f64, right: f64, ulps: u64) -> bool { if left.is_nan() || right.is_nan() { // одно из значений нечисло false } else if left.is_sign_positive() != right.is_sign_positive() { // проверка на +0 == -0 left == right } else { let lbits = left.to_bits(); let rbits = right.to_bits(); if lbits > rbits { ulps >= lbits - rbits } else { ulps >= rbits - lbits } } } ``` Метод `is_nan()` проверяет, что значение является нечислом (_NaN_). Метод `is_sign_positive()` проверяет, что число положительное. Сравнение для чисел с разным знаком нужно для случая, когда один параметр содержит положительный ноль, а другой — отрицательный. В конце вычисляется дистанция между числами, которая сравнивается с допустимым количеством ULP. ULP cравнение отлично работает для близко расположенных чисел с плавающей точкой: ```rust {.example_for_playground .example_for_playground_026} assert!(approx_equal_ulp(0.0, -0.0, 0)); println!("{} == {} with ulps {}", 0.0, -0.0, 0); assert!(approx_equal_ulp(-0.1 - 0.2, -0.3, 1)); println!("{} == {} with ulps {}", -0.1 - 0.2, -0.3, 1); assert!(approx_equal_ulp(1e16, 1.0000000000000016e16, 8)); println!("{} == {} with ulps {}", 1e16, 1.0000000000000016e16, 8); assert!(approx_equal_ulp(5e-324, 0.0, 1)); println!("{:e} == {} with ulps {}", 5e-324, 0.0, 1); ``` Вывод: ``` 0 == -0 with ulps 0 -0.30000000000000004 == -0.3 with ulps 1 10000000000000000 == 10000000000000016 with ulps 8 5e-324 == 0 with ulps 1 ``` ULP cравнение не работает для чисел с разными знаками. А для чисел, которые человек счел бы достаточно близкими, ULP сравнение вернет ложь. Например, наименьшее положительное нормализованное число `2.2250738585072014E-308f64` (константа `f64::MIN_POSITIVE`) находится от `0` более чем на `1000000` ULP единиц: ```rust {.example_for_playground .example_for_playground_027} assert!(!approx_equal_ulp(f64::MIN_POSITIVE, 0.0, 1_000_000)); println!("{:e} != {} with ulps {}", f64::MIN_POSITIVE, 0.0, 1_000_000); ``` В действительности между ними огромное растояние равное `2 ** 52` ULP единиц. Вывод в консоль: ``` 2.2250738585072014e-308 != 0 with ulps 1000000 ``` Функция `distance_ulp()` вычисляет расстояние между двумя действительными числами в ULP единицах. При вычислении расстояния между числами с разным знаком следует учитывать, что сетка чисел с плавающей точкой зеркальная относительно `0`. Если какое-то значение является бесконечным или нечислом, то функция возвращает `u64::MAX`. Требуется реализовать `distance_ulp()`. {.task_text} ```rust {.task_source #rust_chapter_0080_task_0080} fn distance_ulp(first: f64, second: f64) -> u64 { // добавьте реализацию функции } ``` Расстояние между числами с разным знаком есть сумма расстояний каждого числа и нуля. Для вычисления расстояния от отрицательного числа до 0 можно взять модуль числа либо рассчитать расстояние до -0. Для определения, что число является бесконечным или нечислом, следует использовать метод `is_finite()`. {.task_hint} ```rust {.task_answer} fn distance_ulp(first: f64, second: f64) -> u64 { if !first.is_finite() || !second.is_finite() { u64::MAX } else if first.is_sign_positive() != second.is_sign_positive() { distance_ulp(first.abs(), 0.0) + distance_ulp(second.abs(), 0.0) } else { let fbits = first.to_bits(); let sbits = second.to_bits(); if fbits > sbits { fbits - sbits } else { sbits - fbits } } } ``` Числа с плавающей точкой нужно использовать, учитывая их недостатки. Нередко в коммерческом коде можно встретить вещественные числа там, где им не место. Задача про фармацевтический цех — подходящий пример. Вместо `f32` для учета веса можно было бы использовать `u32` и хранить веса в миллиграммах. Максимальное значение `u32::MAX` позволяет хранить 4294967295 мг и это больше 4 тонн, что в несколько раз превышает максимальную грузоподъемность накопительной камеры. В бухгалтерском ПО использование чисел с плавающей точкой — моветон. Для денежных рассчетов используются числа с фиксированной точкой. Есть несколько реализаций таких чисел, например, [rust_decimal](https://crates.io/crates/rust_decimal). ## Заключение - В Rust вещественные числа представлены двумя типами: `f32` и `f64`. Они соответствуют форматам одинарной и двойной точности стандарта [IEEE 754-2008](https://ru.wikipedia.org/wiki/IEEE_754-2008). - С помощью суффиксов `f32` и `f64` можно указать тип литерала дробного числа. По умолчанию используется тип `f64`. - Для чисел с плавающей точкой есть специальныe значения: нечисло (_NaN_) и бесконечность (_Infinity_). - Не каждое вещественное число может быть представлено в формате IEEE 754-2008 без погрешности. - Сетка чисел с плавающей точкой неравномерна: она более густая для чисел с малыми порядками и более редкая для чисел с большими порядками. - Для проверки равенства двух вещественных чисел лучше использовать следующие алгоритмы: cравнение с абсолютным эпсилон, сравнение с относительным эпсилон и ULP сравнение.